|
|
Magnetfelt, fluks og kvantiseringI fysikk som handlar om magnetisme opererer vi med to typar "magnetfelt", H-felt og B-felt. Det første, magnetisk feltstyrke H, kan vi oppfatte som det feltet som blir skapt av ein straum gjennom viklingane i spolen. Dette feltet fyller heile spolen. Vi måler i A/m (ampere pr meter). Om vi plasserer ein materialprøve av eit eller anna slag inne i denne spolen, kan vi tenke oss at H-feltet trengjer gjennom prøven over alt. Dette medfører i sin tur at prøven vi har lagt inn i spolen blir magnetisert, anten fordi elementærmagnetar i prøven blir innretta av H-feltet, og/eller fordi det oppstår elektriske straumar i prøven slik at den blir som ein magnet, eller "magnetspole" i seg sjølv. For magnetiseringa av prøven brukar vi symbolet M. Magnetiseringa har same dimensjon som H, altså A/m. Resultatet er at prøven vi studerer, opplever å innehalde summen av feltet H og magnetiseringa M. Summen av desse størrelsane definerer det vi kallar flukstettleik B. B er altså proporsjonal med summen (H+M). Vi skriv relasjonen mellom desse magnetiske storleikane som B= der konstanten kallast permeabiliteten for vakuum, og har verdien = 4 x 10-7 H/m, ( NB!: H står i dette siste tilfellet for SI-eininga henry, og ikkje feltet H). Teikn opp spolen med prøve og felt, og vis der storleikane B, H og M. Relasjonen mellom desse storleikane seier altså kor stor flukstettleik, B, vi får i materialet når det blir utsett for feltet H og samtidig blir magnetisert av dette, med ein styrke M (som vil vere avhengig av H). Feltet B måler vi i eininga tesla, T. For å forstå kva dette feltet inneber, må vi innføre omgrepet magnetisk fluks. B-feltet som vi omtala ovanfor, er eit mål for fluks pr areal. Faraday innførde sine berømte feltlinjer som fiktive kurver som for det første viste retningen av B-feltet på kvar stad i rommet vi studerer, og slik at flukstettleiken B er uttrykt ved antal feltlinjer pr m2 som kryssar eit visst areal. Som sagt er desse linjene berre tenkte, eller fiktive linjer som ikkje har nokon form for reell eksistens. Dei er berre eit hjelpemiddel. Men dei gjer det mogeleg å lage seg biletlege forestillingar om B-feltet. La oss her stanse og tenke over spørsmålet: Kva er eit sterkt eller veikt magnetfelt? Eit godt døme på eit veikt felt er jordfeltet som er ca. 0.5 x 10-4 tesla. Eit godt mål for eit relativt sterkt felt er 1 tesla, mellom anna fordi dette typisk er det feltet vi får ved å magnetisere jern. Likevel skal vi vere klar over at det er råd å skape mykje sterkare felt enn dette. Med superleiarspole kan ein skape felt på over 20 tesla, og ved bruk av konvensjonell elektromagnet, kombinert med superleiarspole, kan ein nå opp mot 50 tesla i dag, i statisk felt. I tillegg kan ein nå opp til fleire hundre tesla ved kortvarige pulseksperiment. Noko heilt spesielt skjer når ein superleiar av det vi kallar type II blir magnetisert ved hjelp av H-feltet: Så lenge H < Hc1 er superleiaren i Meissner fasen (sjå definisjonen av denne i eigen tekst). Men blir H auka over ein viss verdi Hc1 skjer følgjande: Nå oppstår det flukslinjer, som er reelle objekt i form av superstraumkvervlar som går gjennom prøven på liknande måte som Faraday-linjer. Den viktige skilnaden er nå at desse linjene er fysiske objekt, medan Faraday-linjer er tenkte linjer. Og det aller viktigaste: Kvar av flukslinjene inneheld ei viss kvantisert mengde magnetisk fluks . Superstraumen som sirkulerer tapsfritt omkring sentrum av flukslinja, verkar som om den var ein straumspole. Og kvar flukslinje inneheld nøyaktig same mengde magnetisk fluks. Vi seier då at fluksen er kvantisert. Denne kvantiserte mengda fluks er:
der h er Plancks konstant, og e er elektrisk elementærladning. At dette er ei svært lita mengde fluks kan vi forvisse oss om ved å tenke den fordelt over til dømes 1 cm2 areal, og rekne ut kva B-felt dette ville gje. Svaret er
B= dvs. 7 størrelsesordnar mindre enn jordas magnetfelt! Dermed ser vi og grunnen til at det skal eit slikt kollossalt stort antal flukslinjer til for å kvantisere eit felt på til dømes 1 tesla. Eit slikt felt, over eit areal 1 cm2 vil skape av storleiksorden 500 milliardar flukslinjer. Alle desse er fysiske objekt som trenger gjennom heile prøven. Grunnen til at dette likevel ikkje nødvendigvis "drep" superleiing, er at den tilnærma normale kjernen i flukslinjene har så liten diameter: I høg-Tc material er den av storleiksorden nanometer, altså nær atomær skala. Då blir det plass til svært mange flukslinjer! Vidare drøfting av kvantisert fluks finn du i dialogen i Shockwave. |
|
|
|
|
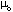 (H+M)
(H+M)
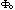 = h/2e
= h/2e