|
|
Meissner-effektenLondon-modellen for Meissner-effektenBrødrene Fritz og Heinz London arbeidde med å forstå Meissner-effekten på 1930-talet. Dei innsåg at i ein superleiar må dei vanlege elektrodynamiske likningane modifiserast, samstundes som Maxwells likningar framleis må vere gyldige. Dette betyr mellom anna at Ohms lov
ikkje lenger gjeld. Dei brukte ein såkalla to-væske modell,
dvs at dei frie ladningane i superleiaren med total tettleik n blir
delte inn i "normale" ladningar med tettleik nn
med same eigenskapane som i normal fase, og superleiande elektron med
tettleik ns. Dei postulerte at desse
"superelektrona" ikkje blir utsette for spreiingsprosessar
via gittersvingingar (fonon) og defektar, og at dei dermed ikkje gjev
bidrag til resistansen i materialet. Dermed vil dei bli fritt
akselererte av eit eventuelt elektrisk felt. Dersom dei har fart
Superleiande straumtettleik blir dermed
Tar vi den tidsderiverte av denne likninga, og kombinerer denne med (1) får vi
Vi tar så
Her har vi ført inn størrelsen h som eit mål for
Dette er Londons elektrodynamiske likning for superleiar. Spørsmålet er nå om denne likninga vil gje oss det observerte fenomenet at magnetisk fluks blir kasta ut av superleiaren. Vi skal vise dette ved å bruke Maxwells likning
Vi tar
Denne likninga kan vi skrive om til følgjande:
der parameteren
Vi skriv ut
Vi står att med
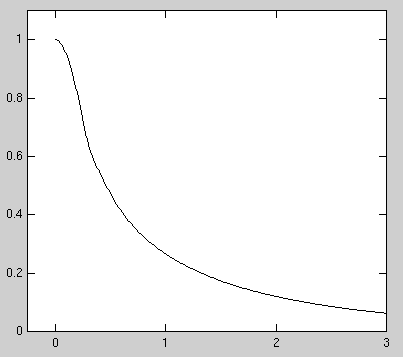
Denne kan nå brukast til å rekne ut feltfordelinga i superleiaren, slik at vi kan få svar på om Meissner-effekten er til stades. La oss prøve: Anta at vi ser på feltfordelinga i eit snitt gjennom ein prøve som strekker seg frå x = 0. Vi spør om feltet i det heile tenger inn i materialet i superleiande tilstand, og ventar at svaret skal vere i samsvar med observasjon. Likning (10) blir nå:
Vi antar at feltet utanfor superleiaren er h0. Vi får nå at
Tilsvarande gjeld
Dersom
Men her kjem eit viktig tilleggspoeng: To-væskemodellen seier at
når vi går frå ein temperatur langt under Tc (Tc
er temperaturen der superleiing først opptrer ved avkjøling) mot
Tc, så minkar ns gradvis, og går til null ved
Tc. Og ns er null ved alle temperaturar over
Tc. (Denne tankegangen er og i samsvar med den moderne
BCS-teorien. Men denne ligg på eit anna nivå av kvantefysisk tenking
som vi ikkje skal ta for oss her.) Det som er viktig å konstatere, er
at når ns går mot null, går
Tenker vi gjennom resultatet den andre vegen, altså ved avkjøling,
har vi funne at feltet er inne i heile prøven over Tc, men
blir pressa ut av prøven under Tc fordi
Magnetisering i Meissner-fasen
I eksperimentet der superleiaren svevar over magneten ved lågt
felt, er årsaka å finne i dei forholda som er diskutert under
London-modellen. Anomasjonane viste at det oppstod ein superstraum
ved Tc og at denne vart pressa ut til overflata av prøven
ved vidare nedkjøling slik at denne vart som ein magnetspole, med eit
felt som akkurat kompenserer for det ytre pålagde feltet, og dermed at
vi fekk null felt totalt inne i prøven. Dette betyr altså at
superstraumen magnetiserer prøven i motsett retning av retningen på
det ytre feltet, og dermed at B = 0 inne i prøven. Likninga
må gjelde. Og skal vi ha B = 0 inne i volumet av prøven, må vi altså ha at
Her er H feltet frå magneten. Det er altså denne magnetiseringa
For ein sylindrisk prøve er det enkel matematikk å vise at relasjonen ovanfor blir til
når vi tar
Vi ser at denne straumen døyr ut over same avstand som h og
B innover i prøven. Igjen er dette ei side ved
Meissner-effekten. Ved å integrere opp det feltet denne straumen
skapar, ville vi og kunne overbevise oss om at resultatet er i samsvar
med at
Det vi har kalla overflatestraum tidlegare, er altså straumen
|
|||||||||||||||||||||||||
|
|
|
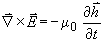 .
Da får vi
.
Da får vi
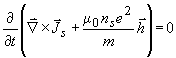
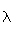 har dimensjon
lengde, og er gitt av
har dimensjon
lengde, og er gitt av
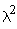 =
m/
=
m/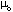 nse2.
nse2.
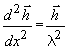
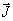 :
: